1. 동적 프로그래밍
2. MDP 모델과 동적 프로그래밍의 적용
3. 평가와 컨트롤
4. 정책 평가(Prediction)
   1. 계산 효율 비교 (행렬 연산 vs 동적 프로그래밍)
5. 컨트롤과 정책 향상
6. 정책 반복과 가치 반복
   1. 정책 반복
   2. 수정된 정책 반복(modified policy iteration)
   3. 가치 반복(value iteration)
   4. 정책 향상과 가치 반복 비교
7. 일반화된 정책 반복
8. 정리
9. 참고

동적 프로그래밍

동적 프로그래밍은 복잡한 최적화 문제를 보다 작은 하위 문제로 분할하여 해결하는 프로그래밍 기술이다.

동적 프로그래밍을 적용하려면 두 가지 핵심 조건을 충족해야 한다:

• 최적 부분 구조(Principle of Optimality): 최적 부분 구조는 큰 문제의 최적 해결책을 구할 때, 큰 문제를 작은 하위 문제들로 나누어 각각의 최적 해결책을 찾고, 이를 조합하여 전체 문제의 해결책을 도출할 수 있다는 것을 의미한다.
• 부분 문제의 재사용: 동일한 하위 문제의 해결책은 여러 번 발생하며, 한번 계산된 결과를 저장하고 재사용함으로써 중복 계산을 피할 수 있다는 원칙이다. 동적 프로그래밍에서는 이를 이용하여 계산 효율성을 높인다.

MDP 모델과 동적 프로그래밍의 적용

앞서 설명한 대로 동적 프로그래밍은 문제를 더 작은 문제로 나누고, 최적 해결책을 도출하는 방식이다. 한편, MDP(Markov Decision Process) 모델은 동적 프로그래밍의 두 가지 조건을 만족한다.

MDP에서의 벨만 방정식을 통해 각 상태에서의 최적 가치를 계산하고 최적 행동을 결정할 수 있다. 이 때, 계산된 각 상태의 가치를 메모리에 저장하여 다른 상태의 최적 가치를 계산할 때 재사용할 수 있다. 이를 메모라이제이션(memorization)이라고 한다.

이처럼, MDP 모델에서는 벨만 방정식의 특징과 동적 프로그래밍을 이용하여 최적 정책을 탐색할 수 있다.

평가와 컨트롤

• 평가(Prediction): 주어진 정책의 성능을 평가한다.
• 컨트롤(Control): 최적의 정책을 찾는 과정이다. 평가 과정은 컨트롤 과정에 포함되는 경우가 많다. 중간 중간 평가를 하면서 최적을 찾아가기 때문이다.

정책 평가(Prediction)

정책 평가는, 주어진 정책이 얼마나 좋은지 측정하는 과정으로, 벨만 기대 방정식을 사용하여 각 상태의 가치를 계산한다. 상태가치값은 ‘정책의 좋음’을 평가하는 가치로 사용되고, 정책을 향상시키는 단계에서도 중요한 정보가 된다.

정책 평가는 벨만 기대 방정식을 사용하여 수행할 수 있다.

계산 효율 비교 (행렬 연산 vs 동적 프로그래밍)

MDP 모델을 MRP로 치환한다음 행렬 연산을 통해 계산할 수도 있지만, 상태의 수가 많아질 경우 연산량이 너무 많아질 수 있다. 일반적으로 상태 수에 따른 행렬연산의 시간복잡도는 O(S^3)로 표현된다.

이러한 경우에는 행렬 연산 대신 동적 프로그래밍을 활용하여 효율적으로 계산할 수 있다.

그러나 이것은 어디까지나 일반적인 설명을 위한 것이다. 계산의 효율이라는 것은 문제 상황이나, 세부 구현 방식에 따라서 달라질 수 있다. 그래서 학습하는 과정에서는 동작 원리에 더 집중을 할 필요가 있다.

예를 들어, 한 블로그 글에서 두 연산에 대해 비교한 내용을 보자. 이 글에서는 피보나치 수열 계산 문제를 예로 들어 비교하였다. 결과적으로 이 비교 실험에서는 행렬 연산이 동적 프로그래밍보다 빠른 연산 시간을 보여준다. 하지만 자세히 들여다보면 행렬 연산을 수행할 때 수열을 단계적으로 계산해 나가면서, 이전에 계산한 내용을 재사용했고 이는 동적 프로그래밍의 중요한 특징을 적용한 것이다.

이 외에도 행렬 연산을 최적으로 수행하기 위해 동적 프로그래밍 기법을 적용한 Matrix Chain Multiplication 등도 있다. 이에 대해서는 추후에 학습하고 정리해야 겠다.

컨트롤과 정책 향상

컨트롤 과정에서는 정책 향상(policy improvement)을 통해 보다 좋은 정책으로 이동한다. 이 과정에서 탐욕 정책 향상(greedy policy improvement) 방법이 자주 사용된다.

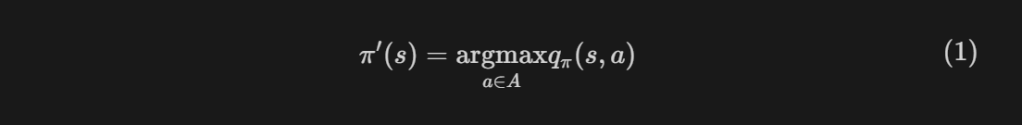
탐욕 정책 향상에서는 위 식(1)에 의해서 새로운 정책을 선택한다. 탐욕 정책 향상에서는 결정적 선택(deterministic)만을 다루는데, 그 이유는 식을 보면 알 수 있다:

• 식을 보면 행동가치값을 사용하여 항상(결정적으로) 행동 가치값을 최대화하는 행동만을 선택하기 때문이다.

정책의 평가 과정에서는 상태가치값을 사용하지만 탐욕 연산에서는 행동가치값을 사용한다. 이 문제는 행동가치값과 상태가치값과의 관계(아래 식(2)참조)를 통해 해결할 수 있다.

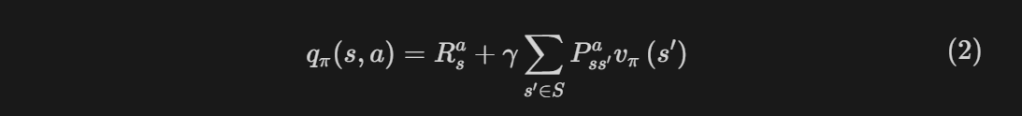
정책을 향상하기 위해서는 어떤 정책이 더 좋은 정책인지를 정의해야한다. 더 좋은 정책의 정의는 다음과 같다:

• 모든 상태 s, s`에 대해 정책π의 상태 가치값이 큰 경우 더 좋은 정책이다.

그렇다면 탐욕 정책 향상을 사용하면 위에서 본 정의에 맞는, 더 좋은 정책을 얻을 수 있을까? 답은 ‘맞다’이다. 이에 대한 증명 과정이 궁금하다면 이 글을 참조하면 좋을 것 같다.

정책 반복과 가치 반복

최적의 정책을 찾기 위한 두 가지 방법으로 정책 반복(Policy Iteration)과 가치 반복(Value Iteration)이 있다. 이 방법들은 정책 평가와 정책 향상 단계를 반복하며 최적의 정책을 도출한다.

정책 반복

다음의 두 단계를 번갈아 수행하면서 정책이나 가치값의 변화가 없을 때까지 수행해 최적의 정책을 구한다:

1. 정책 평가 : 상태가치값을 계산하여 값이 수렴할 때까지 반복한다.
2. 정책 향상 : 정책 평가에서 사용한 상태가치값을 이용하여 탐욕 연산을 수행하고 정책을 향상 시킨다.

수정된 정책 반복(modified policy iteration)

앞에서는 상태가치값이 수렴할 때까지 계산을 반복하였지만, 이 경우 계산이 너무 오래 걸리 문제가 있다.

한편, 어느 정도 수준까지만 정책 향상을 수행해도 동일한 결과를 생성함이 알려져 있다. 그 의미는 반드시 상태가치값이 수렴할 때까지 반복하지 않고, k번(적당히) 반복하여도 최적 정책을 구할 수 있다는 것이다. 이를 수정된 정책 반복이라고 한다.

자세한 내용은 Modified policy iteration algorithms for discounted Markov decision problems[1]을 참조할 수 있다. 이에 대해서도 따로 학습을 해봐야겠다.

가치 반복(value iteration)

가치 반복은 앞서 확인한 정책 반복과 달리, 정책 평가와 정책 향상의 단계를 구분하지 않고 한 개의 식으로 결합한 방법이며, 식은 다음과 같다.

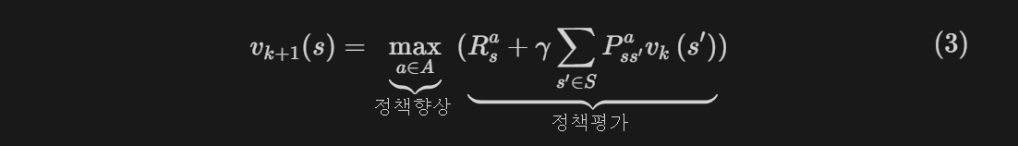
가치 반복에서는 모든 상태에 대한 최적 가치 함수를 계산하고, 각 상태에서 가능한 모든 행동을 고려하여 가장 높은 가치를 주는 행동을 선택한다.

정책 향상과 가치 반복 비교

1. 정책 반복에서는 정책 평가와 향상을 분리된 단계로 반복하지만, 가치 반복에서는 이 두 단계를 하나의 반복 과정으로 본다.
2. 정책 반복은 정책 평가 단계에서 정책을 고정한 상태로, 즉 정책에 의한 행동 하나만 선택하여 상태 가치를 계산한다. 가치 반복은 각 상태에서 가능한 모든 행동에 대한 가치값을 고려하여 상태 가치값을 최대화하도록 업데이트한다.
3. 일반적으로 가치 반복이 정책 반복에 비해 빠르게 수렴한다. 하지만 문제 상황과, 구현 방식에 따라 다를 수 있다.

두 개념에 대해서 잘 비교, 정리한 글이 있어서 소개한다. 아래 참고 글에서 두 알고리즘의 수도(pseudo) 코드도 확인할 수 있다.

참고 : https://www.baeldung.com/cs/ml-value-iteration-vs-policy-iteration

일반화된 정책 반복

일반화된 정책 반복(generalized policy iteration)은 정책 평가와 정책 향상을 다양한 수준에서 수행할 수 있는 방식임을 의미한다.

정책 평가의 측면에서는 다음과 같이 여러 수준의 계산 방식이 있다:

1. 전체 가치값을 수렴할 때까지 반복 계산
2. 전체 가치값을 한 단계만 계산
3. 전체 가치값의 일부만을 계산

정책 향상에서도 마찬가지로 여러 수준의 계산 방식이 있다:

1. 전체 상태에 대해 새로운 행동 탐색
2. 일부 상태에 대해서만 새로운 행동을 선택

정리

MDP 모델의 벨만 방정식은 동적 프로그래밍의 두 조건을 만족하며, 따라서 이를 이용하여 최적 정책을 구할 수 있다.

이 방법은 보상과 전이 확률과 같은 환경 변수가 알려진 모델 기반에서만 사용할 수 있다.

최적 정책을 찾기 위해서, 현재 정책을 평가(1)하고 향상(2)시키는 과정을 반복한다.

정책 평가는 MDP모델을 MRP모델로 치환하여 벨만 기대 방정식을 이용하여 행렬 연산을 수행하거나, 벨만 기대 방정식을 반복적으로 계산하여 가치값을 계산할 수 있다.

정책 향상을 위해서는 정책 반복, 가치값 반복을 활용할 수 있다. 이때, 정책 반복에서 반드시 가치값들이 수렴할 때까지 계산하지 않고 중간값을 사용해도 되며, 이를 활용하여 수행 속도를 향상시킬 수 있다.

정책 반복은 다양한 알고리즘을 활용하여 구현할 수 있으며, 이를 일반화된 정책 반복이라고 한다.

참고

참고 도서

1. 이창환. (2023). 심층강화학습. 도서출판 홍릉

참고 논문

[1] Puterman, M. L., & Shin, M. C. (1978). Modified policy iteration algorithms for discounted Markov decision problems. Management Science, 24(11), 1127-1137.

외부 글

1. Dynamic Programming vs. Transformation Matrix in Linear Recurrence problems
2. Policy Improvement Theorem
3. Value Iteration vs. Policy Iteration in Reinforcement Learning

이 블로그의 관련 글

[강화학습] Markov Decision Process